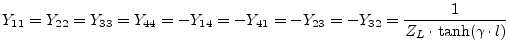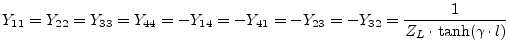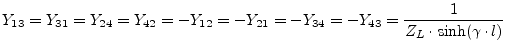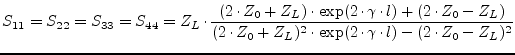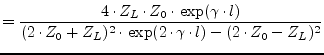Differential Transmission Line

A differential (4-port) transmission line is not referenced to ground potential, i.e. the wave from the input (port 1 and 4) is distributed to the output (port 2 and 3). Its admittance parameters are:

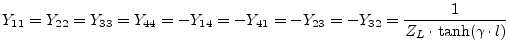$$Y_{11} = Y_{22} = Y_{33} = Y_{44} = -Y_{14} = -Y_{41} = -Y_{23} = -Y_{32} = \dfrac{1}{Z_L \cdot \tanh(\gamma\cdot l)}$$ (9.210)

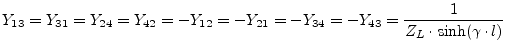$$Y_{13} = Y_{31} = Y_{24} = Y_{42} = -Y_{12} = -Y_{21} = -Y_{34} = -Y_{43} = \dfrac{1}{Z_L \cdot \sinh(\gamma\cdot l)}$$ (9.211)

The scattering parameters writes:

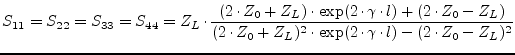$$S_{11} = S_{22} = S_{33} = S_{44} = Z_L \cdot \dfrac{(2\cdot Z_0 ... ...)} {(2\cdot Z_0 + Z_L)^2\cdot \exp(2\cdot\gamma\cdot l) - (2\cdot Z_0 - Z_L)^2}$$ (9.212)

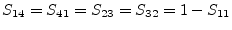$$S_{14} = S_{41} = S_{23} = S_{32} = 1 - S_{11}$$ (9.213)

$$S_{12} = S_{21} = S_{34} = S_{43} = -S_{13} = -S_{31} = -S_{24} = -S_{42}$$ (9.214)

$$= \dfrac{4\cdot Z_L \cdot Z_0 \cdot \exp(\gamma\cdot l)} {(2\cdot Z_0 + Z_L)^2\cdot \exp(2\cdot\gamma\cdot l) - (2\cdot Z_0 - Z_L)^2}$$ (9.215)

Note: As already stated, this is a pure differential transmission line without ground reference. It is not a three-wire system. I.e. there is only one mode. The next section describes a differential line with ground reference.