![\includegraphics[width=0.9\linewidth]{cpline}](img2428.png)
|
A coplanar line is a structure in which all the conductors supporting wave propagation are located on the same plane, i.e. generally the top of a dielectric substrate. There exist two main types of coplanar lines: the first, called coplanar waveguide (CPW), that we will study here, is composed of a median metallic strip separated by two narrow slits from a infinite ground plane, as may be seen on the figure below.
The characteristic dimensions of a CPW are the central strip width ![]() and the width of the slots
and the width of the slots ![]() . The structure is obviously
symmetrical along a vertical plane running in the middle of the
central strip.
. The structure is obviously
symmetrical along a vertical plane running in the middle of the
central strip.
The other coplanar line, called a coplanar slot (CPS) is the complementary of that topology, consisting of two strips running side by side.
A CPW can be quasi-statically analysed by the use of conformal mappings. Briefly speaking, it consists in transforming the geometry of the PCB into another conformation, whose properties make the computations straightforward. The interested reader can consult the pp. 886 - 910 of [48] which has a correct coverage of both the theoretical and applied methods. The French reader interested in the mathematical arcanes involved is referred to the second chapter of [49] (which may be out of print nowadays), for an extensive review of all the theoretical framework. The following analysis is mainly borrowed from [39], pp. 375 et seq. with additions from [48].
The CPW of negligible thickness located on top of an infinitely deep
substrate, as shown on the left of the figure below, can be mapped
into a parallel plate capacitor filled with dielectric ![]() using
the conformal function:
using
the conformal function:
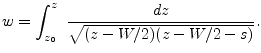 |
(12.1) |
To further simplify the analysis, the original dielectric boundary is
assumed to constitute a magnetic wall, so that ![]() and
and ![]() become
magnetic walls too and there is no resulting fringing field in the
resulting capacitor. With that assumption, the capacitance per unit
length is merely the sum of the top (air filled) and bottom
(dielectric filled) partial capacitances. The latter is given by:
become
magnetic walls too and there is no resulting fringing field in the
resulting capacitor. With that assumption, the capacitance per unit
length is merely the sum of the top (air filled) and bottom
(dielectric filled) partial capacitances. The latter is given by:
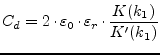 |
(12.2) |
while the former is:
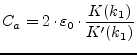 |
(12.3) |
In both formulae ![]() and
and ![]() represent the complete elliptic
integral of the first kind and its complement, and
represent the complete elliptic
integral of the first kind and its complement, and
![]() . While the separate evaluation of
. While the separate evaluation of ![]() and
and ![]() is
more or less tricky, the
is
more or less tricky, the ![]() ratio lets itself compute efficiently
through the following formulae:
ratio lets itself compute efficiently
through the following formulae:
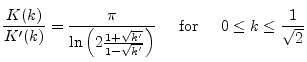 |
(12.4) |
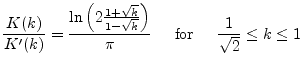 |
(12.5) |
with ![]() being the complementary modulus:
being the complementary modulus:
![]() . While
[48] states that the accuracy of the above formulae is close
to
. While
[48] states that the accuracy of the above formulae is close
to ![]() , [39] claims it to be
, [39] claims it to be
![]() . It can
be considered as exact for any practical purposes.
. It can
be considered as exact for any practical purposes.
The total line capacitance is thus the sum of ![]() and
and ![]() . The
effective permittivity is therefore:
. The
effective permittivity is therefore:
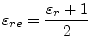 |
(12.6) |
and the impedance:
![\includegraphics[width=0.95\linewidth]{coplanarzl}](img2451.png)
|
In practical cases, the substrate has a finite thickness ![]() . To
carry out the analysis of this conformation, a preliminary conformal
mapping transforms the finite thickness dielectric into an infinite
thickness one. Only the effective permittivity is altered; it
becomes:
. To
carry out the analysis of this conformation, a preliminary conformal
mapping transforms the finite thickness dielectric into an infinite
thickness one. Only the effective permittivity is altered; it
becomes:
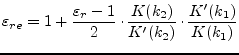 |
(12.8) |
where ![]() is given above and
is given above and
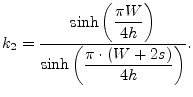 |
(12.9) |
Finally, let us consider a CPW over a finite thickness dielectric backed by an infinite ground plane. In this case, the quasi-TEM wave is an hybrid between microstrip and true CPW mode. The equations then become:
| (12.10) |
where ![]() , called filling factor is given by:
, called filling factor is given by:
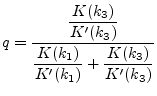 |
(12.11) |
and
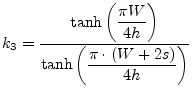 |
(12.12) |
The impedance of this line amounts to:
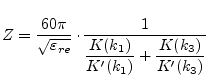 |
(12.13) |
In most practical cases, the strips are very thin, yet their thickness cannot be entirely neglected. A first order correction to take into account the non-zero thickness of the conductor is given by [39]:
| (12.14) |
and
| (12.15) |
where
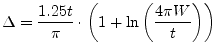 |
(12.16) |
In the computation of the impedance, both the ![]() and the effective
dielectric constant are affected, wherefore
and the effective
dielectric constant are affected, wherefore ![]() must be substituted
by an ``effective'' modulus
must be substituted
by an ``effective'' modulus ![]() , with:
, with:
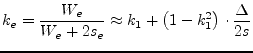 |
(12.17) |
and
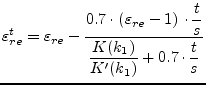 |
(12.18) |
The effects of dispersion in CPW are similar to those encountered in
the microstrip lines, though the net effect on impedance is somewhat
different. [39] gives a closed form expression to compute
![]() from its quasi-static value:
from its quasi-static value:
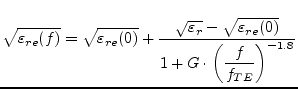 |
(12.19) |
where:
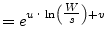 |
(12.20) | |
| (12.21) | ||
| (12.22) | ||
| (12.23) |
and ![]() is the cut-off frequency of the
is the cut-off frequency of the ![]() mode, defined by:
mode, defined by:
| (12.24) |
This dispersion expression was first reported by [50] and
has been reused and extended in [51]. The accuracy of
this expression is claimed to be better than 5% for
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
As for microstrip lines, the losses in CPW results of at least two
factors: a dielectric loss ![]() and conductor losses
and conductor losses
![]() . The dielectric loss
. The dielectric loss ![]() is identical to the
microstrip case, see eq. (11.79) on page
is identical to the
microstrip case, see eq. (11.79) on page
![[*]](crossref.png) .
.
The
![]() part of the losses is more complex to evaluate. As
a general rule, it might be written:
part of the losses is more complex to evaluate. As
a general rule, it might be written:
![$\displaystyle \alpha_c^{CW} = 0.023\cdot \dfrac{R_s}{Z_{0cp}}\left[\dfrac{\part...
...W} - \dfrac{\partial Z^a_{0cp}}{\partial t}\right] \textrm{ in dB/unit length }$](img2481.png) |
(12.25) |
where ![]() stands for the impedance of the coplanar waveguide
with air as dielectric and
stands for the impedance of the coplanar waveguide
with air as dielectric and ![]() is the surface resistivity of the
conductors (see eq. (11.81) on page
is the surface resistivity of the
conductors (see eq. (11.81) on page ![[*]](crossref.png) ).
).
Through a direct approach evaluating the losses by conformal mapping of the current density, one obtains [39], first reported in [52] and finally applied to coplanar lines by [53]:
![\begin{displaymath}\begin{split}\alpha_c^{CW} = &\; \dfrac{R_s\cdot \sqrt{\varep...
...k_1\right)}{t\cdot\left(1+k_1\right)}\right]\right) \end{split}\end{displaymath}](img2484.png) |
(12.26) |
In the formula above,
![]() and it is assumed that
and it is assumed that
![]() and
and ![]() .
.
The computation of the coplanar waveguide lines S- and Y-parameters is
equal to all transmission lines (see section
section 9.20 on page ![[*]](crossref.png) ).
).