Dense matrix class implementation. More...
#include <assert.h>#include <stdio.h>#include <cstdlib>#include <string.h>#include <cmath>#include "logging.h"#include "object.h"#include "complex.h"#include "vector.h"#include "matrix.h"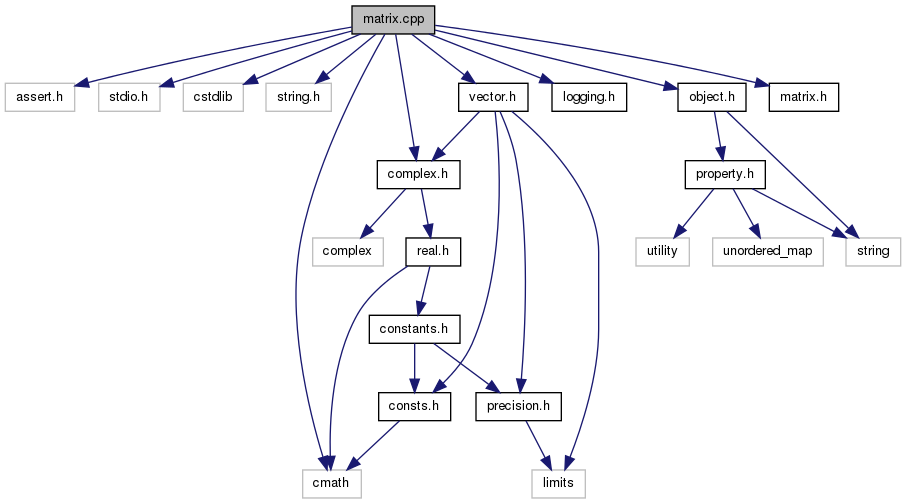
Go to the source code of this file.
Namespaces | |
| namespace | qucs |
Functions | |
| matrix | qucs::operator+ (matrix a, matrix b) |
| Matrix addition. | |
| matrix | qucs::operator- (matrix a, matrix b) |
| Matrix subtraction. | |
| matrix | qucs::operator* (matrix a, nr_complex_t z) |
| Matrix scaling complex version. | |
| matrix | qucs::operator* (nr_complex_t z, matrix a) |
| Matrix scaling complex version (different order) | |
| matrix | qucs::operator* (matrix a, nr_double_t d) |
| Matrix scaling complex version. | |
| matrix | qucs::operator* (nr_double_t d, matrix a) |
| Matrix scaling real version (different order) | |
| matrix | qucs::operator/ (matrix a, nr_complex_t z) |
| Matrix scaling division by complex version. | |
| matrix | qucs::operator/ (matrix a, nr_double_t d) |
| Matrix scaling division by real version. | |
| matrix | qucs::operator* (matrix a, matrix b) |
| matrix | qucs::operator+ (matrix a, nr_complex_t z) |
| Complex scalar addition. | |
| matrix | qucs::operator+ (nr_complex_t z, matrix a) |
| Complex scalar addition different order. | |
| matrix | qucs::operator+ (matrix a, nr_double_t d) |
| Real scalar addition. | |
| matrix | qucs::operator+ (nr_double_t d, matrix a) |
| Real scalar addition different order. | |
| matrix | qucs::operator- (matrix a, nr_complex_t z) |
| Complex scalar substraction. | |
| matrix | qucs::operator- (nr_complex_t z, matrix a) |
| Complex scalar substraction different order. | |
| matrix | qucs::operator- (matrix a, nr_double_t d) |
| Real scalar substraction. | |
| matrix | qucs::operator- (nr_double_t d, matrix a) |
| Real scalar substraction different order. | |
| matrix | qucs::transpose (matrix a) |
| Matrix transposition. | |
| matrix | qucs::conj (matrix a) |
| Conjugate complex matrix. | |
| matrix | qucs::adjoint (matrix a) |
| adjoint matrix | |
| matrix | qucs::abs (matrix a) |
| Computes magnitude of each matrix element. | |
| matrix | qucs::dB (matrix a) |
| Computes magnitude in dB of each matrix element. | |
| matrix | qucs::arg (matrix a) |
| Computes the argument of each matrix element. | |
| matrix | qucs::real (matrix a) |
| Real part matrix. | |
| matrix | qucs::imag (matrix a) |
| Imaginary part matrix. | |
| matrix | qucs::sqr (matrix a) |
| Multiply a matrix by itself. | |
| matrix | qucs::eye (int rs, int cs) |
| Create identity matrix with specified number of rows and columns. | |
| matrix | qucs::eye (int s) |
| Create a square identity matrix. | |
| matrix | qucs::diagonal (qucs::vector diag) |
| Create a diagonal matrix from a vector. | |
| matrix | qucs::pow (matrix a, int n) |
| nr_complex_t | qucs::cofactor (matrix a, int u, int v) |
| Computes the complex cofactor of the given determinant. | |
| nr_complex_t | qucs::detLaplace (matrix a) |
| Compute determinant of the given matrix using Laplace expansion. | |
| nr_complex_t | qucs::detGauss (matrix a) |
| Compute determinant Gaussian algorithm. | |
| nr_complex_t | qucs::det (matrix a) |
| Compute determinant of the given matrix. | |
| matrix | qucs::inverseLaplace (matrix a) |
| Compute inverse matrix using Laplace expansion. | |
| matrix | qucs::inverseGaussJordan (matrix a) |
| Compute inverse matrix using Gauss-Jordan elimination. | |
| matrix | qucs::inverse (matrix a) |
| Compute inverse matrix. | |
| matrix | qucs::stos (matrix s, qucs::vector zref, qucs::vector z0) |
| S params to S params. | |
| matrix | qucs::stos (matrix s, nr_complex_t zref, nr_complex_t z0) |
| S renormalization with all part identic. | |
| matrix | qucs::stos (matrix s, nr_double_t zref, nr_double_t z0) |
| S renormalization with all part identic and real. | |
| matrix | qucs::stos (matrix s, qucs::vector zref, nr_complex_t z0) |
| S renormalization (variation) | |
| matrix | qucs::stos (matrix s, nr_complex_t zref, qucs::vector z0) |
| S renormalization (variation) | |
| matrix | qucs::stoz (matrix s, qucs::vector z0) |
| Scattering parameters to impedance matrix. | |
| matrix | qucs::stoz (matrix s, nr_complex_t z0) |
| Scattering parameters to impedance matrix identic case. | |
| matrix | qucs::ztos (matrix z, qucs::vector z0) |
| Convert impedance matrix scattering parameters. | |
| matrix | qucs::ztos (matrix z, nr_complex_t z0) |
| Convert impedance matrix to scattering parameters identic case. | |
| matrix | qucs::ztoy (matrix z) |
| impedance matrix to admittance matrix. | |
| matrix | qucs::stoy (matrix s, qucs::vector z0) |
| Scattering parameters to admittance matrix. | |
| matrix | qucs::stoy (matrix s, nr_complex_t z0) |
| Convert scattering pto adminttance parameters identic case. | |
| matrix | qucs::ytos (matrix y, qucs::vector z0) |
| Admittance matrix to scattering parameters. | |
| matrix | qucs::ytos (matrix y, nr_complex_t z0) |
| Convert Admittance matrix to scattering parameters identic case. | |
| matrix | qucs::stoa (matrix s, nr_complex_t z1, nr_complex_t z2) |
| Converts chain matrix to scattering parameters. | |
| matrix | qucs::atos (matrix a, nr_complex_t z1, nr_complex_t z2) |
| Converts chain matrix to scattering parameters. | |
| matrix | qucs::stoh (matrix s, nr_complex_t z1, nr_complex_t z2) |
| Converts scattering parameters to hybrid matrix. | |
| matrix | qucs::htos (matrix h, nr_complex_t z1, nr_complex_t z2) |
| Converts hybrid matrix to scattering parameters. | |
| matrix | qucs::stog (matrix s, nr_complex_t z1, nr_complex_t z2) |
| matrix | qucs::gtos (matrix g, nr_complex_t z1, nr_complex_t z2) |
| matrix | qucs::ytoz (matrix y) |
| Convert admittance matrix to impedance matrix. | |
| matrix | qucs::cytocs (matrix cy, matrix s) |
| Admittance noise correlation matrix to S-parameter noise correlation matrix. | |
| matrix | qucs::cstocy (matrix cs, matrix y) |
| Converts S-parameter noise correlation matrix to admittance noise correlation matrix. | |
| matrix | qucs::cztocs (matrix cz, matrix s) |
| Converts impedance noise correlation matrix to S-parameter noise correlation matrix. | |
| matrix | qucs::cstocz (matrix cs, matrix z) |
| Converts S-parameter noise correlation matrix to impedance noise correlation matrix. | |
| matrix | qucs::cztocy (matrix cz, matrix y) |
| Converts impedance noise correlation matrix to admittance noise correlation matrix. | |
| matrix | qucs::cytocz (matrix cy, matrix z) |
| Converts admittance noise correlation matrix to impedance noise correlation matrix. | |
| matrix | qucs::twoport (matrix m, char in, char out) |
| Generic conversion matrix. | |
Detailed Description
Dense matrix class implementation.
References:
[1] Power Waves and the Scattering Matrix Kurokawa, K. Microwave Theory and Techniques, IEEE Transactions on, Vol.13, Iss.2, Mar 1965 Pages: 194- 202
[2] A Rigorous Technique for Measuring the Scattering Matrix of a Multiport Device with a 2-Port Network Analyzer John C. TIPPET, Ross A. SPECIALE Microwave Theory and Techniques, IEEE Transactions on, Vol.82, Iss.5, May 1982 Pages: 661- 666
[3] Comments on "A Rigorous Techique for Measuring the Scattering Matrix of a Multiport Device with a Two-Port Network Analyzer" Dropkin, H. Microwave Theory and Techniques, IEEE Transactions on, Vol. 83, Iss.1, Jan 1983 Pages: 79 - 81
[4] Arbitrary Impedance "Accurate Measurements In Almost Any Impedance Environment" in Scropion Application note Anritsu online(2007/07/30) http://www.eu.anritsu.com/files/11410-00284B.pdf
[5] Conversions between S, Z, Y, H, ABCD, and T parameters which are valid for complex source and load impedances Frickey, D.A. Microwave Theory and Techniques, IEEE Transactions on Vol. 42, Iss. 2, Feb 1994 pages: 205 - 211 doi: 10.1109/22.275248
[6] Comments on "Conversions between S, Z, Y, h, ABCD, and T parameters which are valid for complex source and load impedances" [and reply] Marks, R.B.; Williams, D.F.; Frickey, D.A. Microwave Theory and Techniques, IEEE Transactions on, Vol.43, Iss.4, Apr 1995 Pages: 914- 915 doi: 10.1109/22.375247
[7] Wave Techniques for Noise Modeling and Measurement S. W. Wedge and D. B. Rutledge, IEEE Transactions on Microwave Theory and Techniques, vol. 40, no. 11, Nov. 1992. pages 2004-2012, doi: 10.1109/22.168757 Author copy online (2007/07/31) http://authors.library.caltech.edu/6226/01/WEDieeetmtt92.pdf
Definition in file matrix.cpp.
 1.7.6.1
1.7.6.1